Les électrons et trous jouent un rôle essentiel dans le transfert d'électricité en semi-conducteurs . Ces particules sont disposées à un niveau d'énergie différent dans un semi-conducteur. Le mouvement des électrons d'un niveau d'énergie à un autre produit de l'électricité . Un électron à l'intérieur du métal doit posséder un niveau d'énergie au moins supérieur à l'énergie de la barrière de surface pour s'échapper vers un niveau d'énergie plus élevé.
De nombreuses thèses ont été proposées et acceptées expliquant les caractéristiques et le comportement des électrons. Mais certains comportements d'électrons comme l'indépendance du courant d'émission sur la température etc… restaient encore un mystère. Puis une statistique de rupture, Statistiques de Fermi Dirac , publié par Enrico Fermi et Paul Dirac en 1926 a aidé à résoudre ces énigmes.
À partir de là Distribution de Fermi Dirac est appliquée pour expliquer l'effondrement d'une étoile à une naine blanche, pour expliquer l'émission d'électrons libres des métaux, etc.
Distribution de Fermi Dirac
Avant d'entrer dans le Fonction de distribution de Fermi Dirac regardons l'énergie distribution d'électrons dans divers types de semi-conducteurs. L'énergie maximale qu'un électron libre peut avoir dans un matériau à température absolue. à 0k est connu comme le niveau d'énergie de Fermi. La valeur de l'énergie de Fermi varie pour différents matériaux. Sur la base de l'énergie possédée par les électrons dans un semi-conducteur, les électrons sont disposés en trois bandes d'énergie - bande de conduction, niveau d'énergie de Fermi, bande de valence.
Alors que la bande de conduction contient des électrons excités, la bande de valence contient des trous. Mais à quoi sert le niveau de Fermi? Le niveau de Fermi est l'état d'énergie qui a une probabilité de moitié d'être occupé par un électron. En termes simples, c'est le niveau d'énergie maximal qu'un électron peut avoir à 0k et la probabilité de trouver l'électron au-dessus de ce niveau à température absolue est de 0. À température nulle absolue, la moitié du niveau de Fermi sera remplie d'électrons.
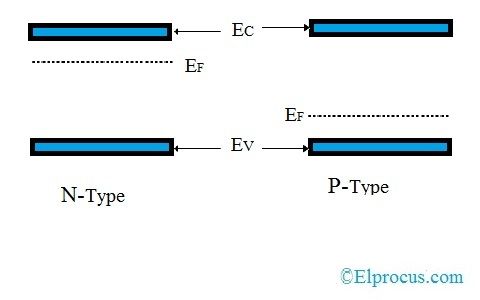
Dans le diagramme de bande d'énergie du semi-conducteur, le niveau de Fermi se situe au milieu de la bande de conduction et de valence pour un semi-conducteur intrinsèque. Pour les semi-conducteurs extrinsèques, le niveau de Fermi se situe près de la bande de valence dans Semi-conducteur de type P et pour Semi-conducteur de type N , il se trouve près de la bande de conduction.
Le niveau d'énergie de Fermi est noté ESTF, la bande de conduction est notée ESTC et la bande de valence est notée EV.

Niveau de Fermi dans les types N et P
Niveau de Fermi dans les semi-conducteurs de type N et P
Fonction de distribution de Fermi Dirac
La probabilité que l’état d’énergie disponible «E» soit occupé par un électron à la température absolue T dans des conditions d’équilibre thermique est donnée par la fonction de Fermi-Dirac. De la physique quantique, l'expression de distribution de Fermi-Dirac est
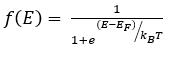
Où k est la constante de Boltzmann dans OUÀ , T est la température en 0À et ESTF est le niveau d'énergie de Fermi en eV.k = 1,38X10-2. 3J / K
Le niveau de Fermi représente l'état énergétique avec une probabilité de 50% d'être rempli s'il n'y a pas de bande interdite, c'est-à-dire si E = EF alors f (E) = 1/2 pour toute valeur de température.
La distribution de Fermi-Dirac ne donne que la probabilité d’occupation de l’état à un niveau d’énergie donné mais ne fournit aucune information sur le nombre d’états disponibles à ce niveau d’énergie.
Distribution de Fermi Dirac et diagramme de bande d'énergie

f (E) contre (E-EF) terrain
Le graphique ci-dessus montre le comportement du niveau de Fermi à différentes plages de température T = 00K, T = 3000K, T = 25000À. À T = 0 K , la courbe a des caractéristiques en escalier.
À T = 00À , le nombre total de niveaux d'énergie occupés par les électrons peut être connu en utilisant la fonction de Fermi-Dirac.
Pour un niveau d'énergie donné E> EF , le terme exponentiel de la fonction de Fermi-Dirac devient 0 et ce qui signifie que la probabilité de trouver le niveau d'énergie occupé de l'énergie supérieure à ESTF est zéro.
Pour un niveau d'énergie donné EST
Pour une température supérieure à la température absolue et E = EF , alors indépendante de la valeur de la température.
Pour une température supérieure à la température absolue et EST
Pour une température supérieure à la température absolue et E> EF , l'exponentielle sera positive et augmente avec E. f (E) commence à 0,5 et tend à diminuer vers 0 lorsque E augmente.
Distribution de Fermi Dirac Approximation de Boltzmann
La distribution de Maxwell-Boltzmann est la Approximation de la distribution de Fermi Dirac .
La distribution de Fermi-Dirac est donnée par 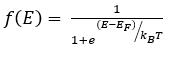
Par en utilisant Maxwell - Approximation de Boltzmann l'équation ci-dessus est réduite à

Lorsque la différence entre l’énergie du porteur et le niveau de Fermi est grande par rapport à, le terme 1 dans le dénominateur peut être négligé. Pour l'application de la distribution de Fermi-Dirac, l'électron doit suivre le principe exclusif de Pauli, ce qui est important en cas de dopage élevé. Mais la distribution de Maxwell-Boltzmann néglige ce principe, l'approximation de Maxwell-Boltzmann est donc limitée aux cas faiblement dopés.
Statistiques de Fermi Dirac et Bose-Einstein
La statistique de Fermi-Dirac est la branche de la statistique quantique, qui décrit la distribution des particules dans des états d'énergie contenant des particules identiques obéissant au principe d'exclusion de Pauli. Puisque les statistiques F-D sont appliquées aux particules avec un spin demi-entier, celles-ci sont appelées fermions.
Un système constitué de particules thermodynamiquement à l'équilibre et identiques, dans l'état de particule unique I, le nombre moyen de fermions est donné par la distribution F-D comme 
où est l'état d'une seule particule je , le potentiel chimique total est noté, àB est la constante de Boltzmann alors que T est la température absolue.
Les statistiques de Bose-Einstein sont à l'opposé des statistiques F-D. Ceci est appliqué aux particules avec un spin entier complet ou sans spin, appelées bosons. Ces particules n’obéissent pas au principe d’exclusion de Pauli, ce qui signifie que la même configuration quantique peut être remplie de plus d’un boson.
Les statistiques F-D et les statistiques Bore-Einstein sont appliquées lorsque l'effet quantique est important et que les particules sont indiscernables.
Problème de distribution de Fermi Dirac
Dans un solide, considérons le niveau d'énergie situé à 0,11 eV sous le niveau de Fermi. Trouvez la probabilité que ce niveau ne soit pas occupé par l'électron?

Problème de distribution de Fermi Dirac
Il s'agit de Distribution de Fermi Dirac . À partir des informations ci-dessus enfin, nous pouvons conclure que les propriétés macroscopiques d'un système peuvent être calculées à l'aide d'une fonction de Fermi-Dirac. Il est utilisé pour connaître l'énergie de Fermi dans les cas de température nulle et finie. Répondons à une question sans aucun calcul, basée sur notre compréhension de la distribution de Fermi-Dirac. Pour un niveau d'énergie E, 0,25 eV en dessous du niveau de Fermi et une température au-dessus de la température absolue, la courbe de distribution de Fermi décroît-elle vers 0 ou augmente-t-elle vers 1?