La calculatrice d'algèbre booléenne est le flux de mathématiques qui comprend des expressions logiques et des variables logiques manipulant. Il exécute le opérations logiques comme AND, NAND, OR, NOR, NOT & X-OR . Les valeurs du calculateur d'algèbre booléenne sont notées avec la logique 0 & 1. Le calculateur d'algèbre booléenne utilise les lois de base comme la loi d'identité, la loi commutative, la loi distributive, la loi d'association et la loi de redondance. Le but principal de cette loi est utilisé pour accomplir les opérations logiques comme l'égalité, la disjonction, la conjonction et l'implication. Les opérations logiques peuvent être énoncées de différentes manières, telles que: la conjonction (a ^ b) est énoncée comme a et b, la disjonction (a V b) est énoncée comme a ou b, l'implication (a b) est énoncée comme un implique b & l'égalité (ab) est exprimée par p x-ni q.

Calculateur d'algèbre booléenne
L'application de l'algèbre booléenne est similaire à un état de commutation électrique qui peut être des valeurs logiques 0 et 1. La calculatrice d'algèbre booléenne donne instantanément le résultat sous la forme d'une expression mathématique en exécutant les opérations telles que l'addition, la multiplication, etc. La calculatrice est très facile et simple à utiliser.Boolean Algebra Calculator Block Diagram
Schéma fonctionnel de la calculatrice d'algèbre booléenne
Le schéma de principe du calculateur d'algèbre booléenne comprend différents blocs comme source de courant , clavier, microcontrôleur et Affichage LED .

Schéma fonctionnel de la calculatrice d'algèbre booléenne
L'alimentation est utilisée pour donner de l'énergie au circuit de la chouette, et elle convertit différentes formes d'énergies telles que les énergies solaire, mécanique et chimique en énergie électrique. Ce projet utilise une énergie de 5 V et qui est donnée au clavier, à l'affichage et au microcontrôleur. Un microcontrôleur est utilisé pour lire les données du clavier et envoie les données au affichage LCD . Le microcontrôleur joue un rôle essentiel dans ce projet et qui est programmé par un Logiciel Wedge .
Dans ce projet, un écran LED à 3 couleurs est utilisé pour afficher le motif lumineux de l'expression. Ces bicolores signifient la normale et les compléments des variables comme les commutateurs. Le clavier de ce projet est utilisé pour donner les termes minimum en i / p, c'est-à-dire chaque chiffre du clavier qui répond à chaque terme minimum.
Circuit de calcul d'algèbre booléenne
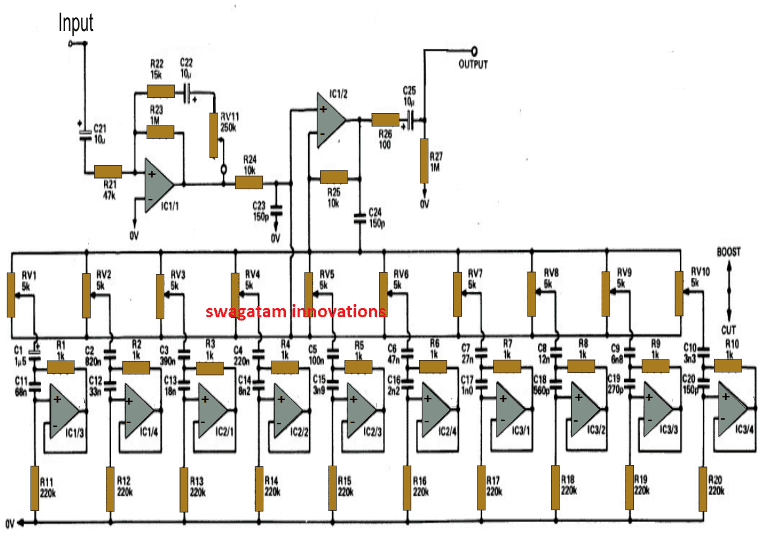
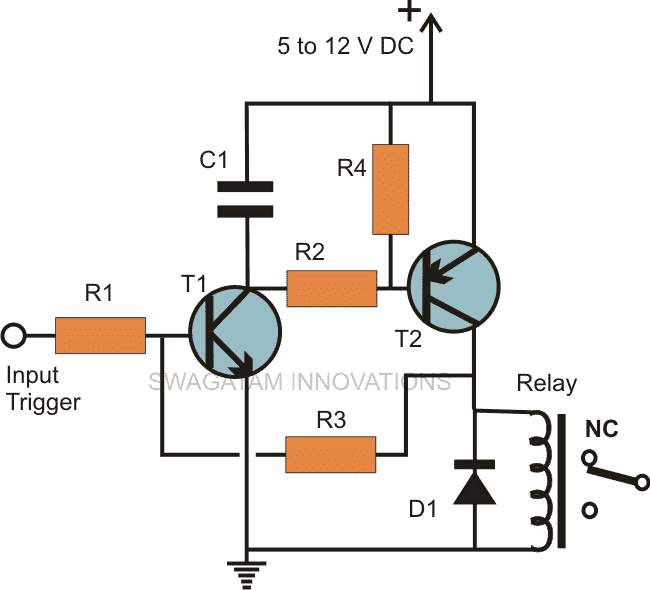
Le schéma de circuit du calculateur d'algèbre booléenne suivant est à faible coût, à faible consommation d'énergie rapide et fiable. Ce circuit est construit avec des composants électriques et électroniques qui sont disponibles sur le marché comme des résistances, un clavier, un écran LCD et un microcontrôleur, comme indiqué dans le circuit suivant.

Circuit de calcul d'algèbre booléenne
Le circuit ci-dessus se compose de trois minimiseurs variables, qui utilisent «l'algorithme Quine MC Cluskey» et trouve la somme minimale des produits en exécutant des fonctions booléennes. Cette calculatrice résout les expressions booléennes et fonctions logiques en utilisant différents théorèmes et lois. Le microcontrôleur utilisé dans ce projet joue un rôle essentiel, qui est codé avec un programme et contrôle les composants utilisés dans ce circuit.
Lorsque l'alimentation est fournie au circuit, la LED clignote. Le clignotement de la LED indique que le microcontrôleur est prêt à recevoir les i / ps du clavier. Ces expressions booléennes sont données sous la forme d'une somme de produits (SOP).
Ce projet utilise un clavier composé de 9 commutateurs, où huit commutateurs liés aux termes minimum qui exécutent l'opération du produit et le commutateur restant est utilisé comme bouton suivant. Lorsque l'expression est entrée, la LED s'éteint et, en fonction de l'algorithme, le microcontrôleur diminue l'expression du terme minimum. Ensuite, le voyant i / p clignote, ce qui signifie que l'expression est minimisée et s'affiche sur le voyant.
Le o / p est affiché comme un terme min à la fois, et le deuxième terme min est affiché en appuyant sur le bouton suivant. Ainsi, après avoir obtenu le dernier terme min, l'expression sera réduite et le voyant i / p s'éteint, ce qui indique que le fonctionnement est terminé, puis automatiquement, le voyant s'allume pour indiquer que le microcontrôleur est prêt à prendre le i / p. p.
Simplification de l'expression booléenne
Les expressions suivantes sont un exemple d'expressions booléennes utilisant des techniques algébriques.
L'expression est ~ (A * B) * (~ A + B) * (~ B + B) = ~ A
- ~ (A * B) * (~ A + B) * (~ B + B)
- La loi d'identité et la loi du complément sont ~ (A * B) * (~ A + B).
- Droit de et De Morgan (~ A ~ + B) * (~ A + B)
- La loi distributive est ~ A + ~ B * B
- ~ A est un compliment ou une identité.
Chaque étape donne une forme d'équation et les règles sont utilisées pour résoudre les équations des équations précédentes. En général, il existe différentes manières d'atteindre le résultat.
Lois de l'algèbre booléenne
Il y a de nombreuses lois à résoudre les expressions booléennes. Les théorèmes d'algèbre booléenne sont notamment Idempotent Associatif, Commutatif, Distributif, Identité, Complément, Involution et DeMorgan.
Loi idempotente
A * A = A
A + A = A
Loi associative
(A * B) * C = A * (B * C)
(A + B) + C = A + (B * C)
Loi commutative
A * B = B * A
A + B = B + A
Loi distributive
A * (B + C) = A * B + A * C
A + (B * C) = A + B * A + C
Loi d'identité
A * 0 = 0 A *! = A
A +! =! A + 0 = A
Loi de compliment
A * ~ A = 0
A + ~ A =!
Loi d'involution
~ (~ A) = A
Loi de DeMorgan
~ (A * B) = ~ A + ~ B
~ (A + B) = ~ A * ~ B
Chaque loi de ce qui précède est décrite par deux parties et c'est duales l'une de l'autre. Le principe de dualité est, en interchangeant les opérations + (OR) et * (AND), les éléments 0 et 1 de l'expression.
Pour une meilleure compréhension du concept de circuit de calculateur d'algèbre booléenne, nous avons expliqué ici une simplification d'algèbre booléenne. L'exemple de simplification de l'algèbre booléenne est expliqué ci-dessous.

Exemple de simplification de l'algèbre booléenne
Le circuit ci-dessus est conçu avec deux portes OU et deux portes NAND, à partir du circuit, nous pouvons obtenir l'équation comme AB + BC (B + C) qui est montrée dans la figure ci-dessus. Lorsque la règle d'identité et la factorisation finale sont appliquées au circuit ci-dessus, l'expression simplifiée prendra la forme de simple.
Ainsi, il s'agit de Algèbre de Boole circuit de calculatrice, diagramme de bloc de calculatrice d'algèbre booléenne, diagramme de circuit de calculatrice d'algèbre booléenne, simplification de l'expression booléenne, lois d'algèbre booléenne et exemple de simplification d'algèbre booléenne. Nous pensons que vous avez une meilleure compréhension de ce concept, en plus des doutes sur ce sujet, veuillez donner votre avis en commentant dans la section des commentaires ci-dessous.Voici une question pour vous, quelles sont les applications du calculateur d'algèbre booléenne?