Le diagramme de Bode et les diagrammes de Nyquist sont des diagrammes très populaires, en particulier pour la spectroscopie d'impédance électrochimique ou les données EIS parmi les électrochimistes. Ainsi, Nyquist Plot porte le nom d'un suédo-américain nommé 'Harry Nyquist'. Il est ingénieur électricien et a développé cette parcelle à des fins électroniques en 1932. Au cours d'un EIS, de nombreuses informations sont collectées et ces informations collectées doivent être présentées. Ainsi, une image donne plus d'informations que cent mots. Ainsi, une représentation graphique comme un tracé de Nyquist est utilisée pour montrer une spectroscopie d'impédance électrochimique. Cet article fournit des informations sur Parcelle de Nyquist – fonctionnement, avantages & ses inconvénients.
Définition du tracé de Nyquist
La représentation graphique largement utilisée pour les fonctions de transfert est connue sous le nom de diagramme de Nyquist. Il s'agit d'un tracé de réponse en fréquence utilisé pour évaluer le système de contrôle avec la stabilité de la rétroaction. Il s'agit d'un tracé paramétrique pour la partie réelle et imaginaire d'une fonction de transfert dans le plan complexe car le paramètre de fréquence balaie un intervalle spécifié. En coordonnées cartésiennes, la partie réelle de la fonction de transfert du tracé de Nyquist est tracée sur l'axe X tandis que la partie imaginaire de la fonction de transfert est tracée sur l'axe Y.
Nyquist Plot est utilisé dans le contrôle automatique ainsi que dans le traitement du signal pour l'analyse de la stabilité, car n'importe qui peut vérifier instantanément si une boucle avec rétroaction négative respecte le principe de stabilité de Nyquist. Si le diagramme de Nyquist de la système de contrôle en boucle ouverte couvre approximativement le point sur l'axe réel après quoi le système équivalent en boucle fermée est instable.
Graphique de tracé de Nyquist
Les diagrammes de diagrammes de Nyquist sont l'extension des diagrammes polaires utilisés principalement pour trouver le systèmes de contrôle en boucle fermée stabilité en changeant simplement 'ω' de −∞ à ∞. Cela signifie que ces tracés sont principalement utilisés pour dessiner la réponse en fréquence totale de la fonction de transfert en boucle ouverte. Le diagramme de Nyquist évalue simplement la stabilité du système de contrôle avec rétroaction. Ainsi, dans un système de coordonnées cartésien, le vrai par de la fonction de transfert est simplement tracé sur l'axe X tandis que la partie imaginaire est simplement tracée sur l'axe Y.
Le tracé de Nyquist similaire peut être expliqué simplement avec des coordonnées polaires, où le gain de la fonction de transfert est la coordonnée radiale et la phase de la fonction de transfert est la coordonnée angulaire équivalente.
L'intrigue de Nyquist peut être comprise en connaissant certaines des terminologies utilisées. Dans le diagramme de Nyquist, un chemin fermé dans un plan complexe est appelé contour.
Chemin de Nyquist
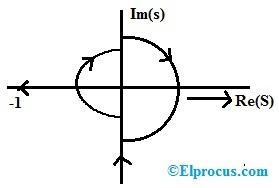
Le chemin de Nyquist ou contour de Nyquist est un contour fermé dans le plan s qui enferme totalement le côté droit complet du plan s. Pour enfermer le RHS total du plan, une grande voie en demi-cercle est dessinée par un diamètre le long de l'axe 'jω' et du centre à la source. Le rayon du demi-cercle est simplement traité comme l'encerclement de Nyquist.

Encerclement de Nyquist
Un point est connu pour être encerclé par une ligne s'il se trouve dans la courbe.
Cartographie de Nyquist
La procédure par laquelle un point dans le plan s est transformé en un point dans le plan F(s) est connue sous le nom de mappage et F(s) est connue sous le nom de fonction de mappage.
L'analyse de stabilité du système de commande par rétroaction dépend principalement de la reconnaissance des racines de localisation de l'équation caractéristique au-dessus du plan s.
Ainsi, si la racine du plan s se trouve sur la face gauche, le système de commandes est stable. Ainsi, la stabilité relative du système peut être déterminée par différentes techniques de réponse en fréquence comme le diagramme de Nyquist, le diagramme de Bode et le diagramme de Nichols.
Critère de stabilité de Nyquist
Le critère de stabilité de Nyquist est principalement utilisé pour reconnaître l'existence de racines pour une équation caractéristique dans la région particulière du plan S. Critère de stabilité de Nyquist comme N = Z - P dit simplement cela. 'N' est le nombre total d'encerclements par rapport à l'origine, 'P' est le nombre de pôles et 'Z' est le nombre total de zéros.
Dans le cas 1 : Lorsque N = 0 (pas d'encerclement), donc Z = P = 0 & Z = P.
Si N = 0, P doit être '0' pour que le système soit stable.
Dans le cas 2 : Lorsque N est supérieur à 0 (encerclement horaire), donc P = 0, Z ≠0 & Z > P
Dans ces deux cas, le système est instable.
Dans le cas 3 : Lorsque N est inférieur à 0 (encerclement dans le sens antihoraire), donc Z = 0, P ≠0 & P > Z
Ainsi, le système est stable.
Comment dessiner un tracé de Nyquist ?
Il y a de nombreuses étapes impliquées dans le dessin du tracé de Nyquist qui sont discutées ci-dessous.
- À l'étape 1 : Besoin de vérifier les pôles pour une fonction de transfert en boucle ouverte comme G(s)H(s) dans le plan « s ».
- À l'étape 2 : Choisissez le contour de Nyquist correct en incluant tout le côté droit du plan s en dessinant simplement un demi-cercle de rayon 'R' où R tend vers l'infini.
- À l'étape 3 : Reconnaître les différents segments sur le contour avec l'emplacement du chemin de Nyquist.
- À l'étape 4 : le segment de mappage doit effectuer le segment en remplaçant simplement l'équation de segment respective dans la fonction de mappage. Généralement, nous devons dessiner les tracés polaires pour le segment particulier.
- A l'étape 5 : Généralement, les segments de cartographie sont des images de réflexion de cartographie pour le trajet particulier de l'axe imaginaire positif.
- À l'étape 6 : La voie semi-circulaire qui couvre la moitié droite du plan correspond normalement à un point dans le plan G(s) H(s).
- À l'étape 7 : Interconnectez tous les différents segments de mappage pour obtenir le diagramme de Nyquist nécessaire.
- À l'étape 8 : notez le no. d'encerclements dans le sens des aiguilles d'une montre autour de (-1, 0) et décider de la stabilité par N = Z - P.
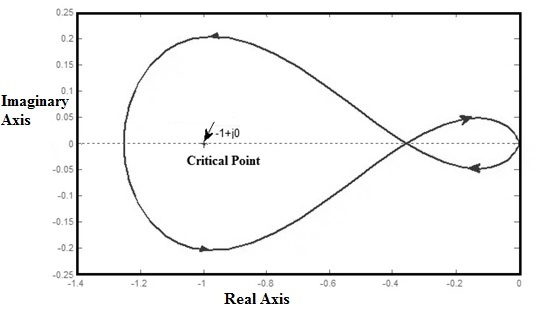
Une fois le tracé de Nyquist tracé, nous pouvons découvrir la stabilité du système de contrôle en boucle fermée avec le critère de stabilité de Nyquist. Ainsi, si le point critique (-1+j0) se trouve à l'extérieur de l'encerclement, alors le système de contrôle en boucle fermée est complètement stable.
La fonction de transfert en boucle ouverte est la G(S)H(S) = N(S)/D(S).
La fonction de transfert en boucle fermée est le G(S)/1+ G(S)H(S).
N(s) = zéro est le zéro de la boucle ouverte et D(s) est le pôle de la boucle ouverte.
Du point de vue de la stabilité, aucun pôle en boucle fermée ne doit se trouver sur la face droite du plan en s. L'équation caractéristique telle que 1 + G(s) H(s) égale à zéro signifie des pôles en boucle fermée.
Lorsque 1 + G(s) H(s) est égal à zéro, alors q(s) doit être égal à zéro.
Ainsi, du point de vue de la stabilité, les zéros de q(s) ne doivent pas se trouver dans le plan de droite du plan s.
Pour décrire la force, l'ensemble du RHP doit être pris en compte. Nous imaginons donc un demi-cercle qui inclut tous les points du RHP en considérant le rayon du demi-cercle « R » qui tend vers l'infini.
Analyse de stabilité avec le diagramme de Nyquist
À partir du diagramme de Nyquist, nous pouvons reconnaître si le système de contrôle est stable, instable ou légèrement stable en fonction des valeurs des paramètres.
- Fréquence de croisement de gain et fréquence de croisement de phase.
- Marge de gain et marge de phase.
Fréquence de croisement de phase.
La fréquence à laquelle le tracé de Nyquist rencontre l'axe réel négatif est appelée fréquence de transition de phase et elle est notée ωpc.
Gain croisé sur la fréquence
La fréquence à laquelle le tracé de Nyquist a une amplitude est appelée fréquence de croisement de gain et elle est notée ωgc.
La stabilité du système de contrôle basée sur la relation principale entre les deux fréquences comme le croisement de phase ainsi que le croisement de gain est discutée ci-dessous.
- Si le ωpc est plus élevé que le ωgc alors le système de contrôle est stable.
- Si le ωpc est équivalent au ωgc alors le système de contrôle est légèrement stable.
- Si le ωpc est inférieur à ωgc alors le système de contrôle n'est pas stable.
Gain de marge
La marge de gain est équivalente à l'inverse de l'amplitude du tracé de Nyquist à la fréquence de transition de phase.
Marge de gain (GM) =1/Mpc
Où 'Mpc' est l'amplitude dans l'échelle normale à la fréquence de transition ωpc ou phase
Marge de phase
La marge de phase est équivalente à la somme de 180 degrés et de l'angle de phase à la fréquence de croisement ωgc ou gain.
PM = 1800 + ϕgc
Où ϕgc est l'angle de phase à la fréquence de croisement du gain (ωgc).
La stabilité du système de contrôle dépend de la relation principale entre les deux marges comme la marge de gain et la marge de phase indiquées ci-dessous.
Si la marge de gain est supérieure à un et que la marge de phase est positive, le système de contrôle est stable.
Si la marge de gain est équivalente à un et que la marge de phase est de 0 degré, le système de contrôle est légèrement stable.
Si la marge de gain est inférieure à un et que la marge de phase est négative, le système de contrôle n'est pas stable.
Problèmes d'exemple de diagramme de Nyquist
Ex1 : Si le diagramme de Nyquist coupe l'axe réel négatif à la distance de 0,6, alors quelle est la marge de gain du système ?
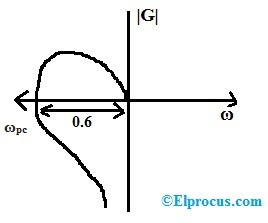
Nous savons que la marge de gain du système peut être définie comme la quantité de changement nécessaire dans le gain en boucle ouverte pour rendre un système en boucle fermée instable est
Marge de gain ou GM = 1/|G| wpc
Où, le gain du système est |G| et wpc est la fréquence de croisement de phase.
La fréquence de croisement de phase peut être définie comme ; la fréquence à laquelle le gain du système est « 0 ».
Gm = 1/0,6 = 1,66
Ex2 : La fonction de transfert du système en boucle ouverte du système de rétroaction négative à gain unitaire peut être donnée par G(s) = 1/S(S+1). La courbe de Nyquist dans le plan S comprend tout le plan du côté droit et une petite zone autour de l'origine du côté gauche illustré dans le graphique suivant. Le non. d'encerclements du point (-1+ j0) par le tracé de Nyquist G(S), équivalent au contour de Nyquist qui est indiqué par 'N' puis 'N' équivalent à ?
Le non. des encerclements pour le (-1+ j0) point significatif est donné par N = P-Z.
Où « N » est le nombre d'encerclements de ce point critique dans le sens inverse des aiguilles d'une montre.
'P' est le nombre de pôles en boucle ouverte dans le côté droit du plan S.
'Z' est le nombre de pôles en boucle fermée dans le côté droit du plan S.
N = P pour la stabilité Z = 0.
La formule ci-dessus n'est valable qu'une fois que la courbe de Nyquist est définie pour le côté droit du plan S et que les pôles sont exclus à la source. La rotation de la courbe doit être dans le sens des aiguilles d'une montre et l'encerclement du point critique est dans le sens inverse des aiguilles d'une montre.
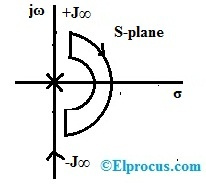
G(s) = 1/S(S+1).
Les pôles en boucle ouverte sont présents à S = 0,-1
La fonction de transfert en boucle fermée = 1/S^2+S+1
Le nombre du pôle fermé sur le côté droit est zéro.
Mais le contour de Nyquist est défini pour la moitié totale du plan S et contient également le pôle à l'origine.
Ainsi, à S = 0, le pôle en boucle ouverte est considéré comme le pôle à l'intérieur du côté droit du plan S.
N = P-Z =>1-0 =>1
Avantages et inconvénients
Le avantages de la parcelle de Nyquist inclure les éléments suivants.
- Le diagramme de Nyquist est un outil extrêmement utile pour déterminer la stabilité du système.
- Il présente de nombreux avantages par rapport au locus Routh-Horwitz & racine car il gère simplement les délais.
- Mais, il est très utile car il nous donne une méthode pour utiliser le diagramme de Bode pour décider de la stabilité.
- En utilisant cela, la stabilité du système de contrôle peut être décidée.
- Une fonction de transfert en boucle ouverte est trouvée en mesurant simplement sa réponse en fréquence.
- Il est meilleur par rapport au locus racine en termes de délai, ce qui signifie que le tracé de Nyquist peut simplement gérer le délai dans le système.
- Il peut localiser la réponse en fréquence de la fonction de transfert en boucle ouverte.
- Il trouve le non. de pôles pôles disponibles sur la face droite du s-plane.
- Il trouve la stabilité relative du système/
Le inconvénients du tracé de Nyquist inclure les éléments suivants.
- Le diagramme de Nyquist utilise des méthodes mathématiques difficiles.
- Il ne peut pas résoudre la force complète du système.
- Il ne donne pas d'informations précises sur les pôles disponibles sur la face droite du plan s.
Demandes pour les parcelles de Nyquist
Les applications du diagramme de Nyquist comprennent les suivantes.
- Le diagramme de Nyquist est utilisé pour établir la stabilité du système par un processus graphique dans le domaine fréquentiel.
- Un tracé de Nyquist ou un tracé de réponse en fréquence est principalement utilisé dans l'ingénierie de contrôle et le traitement du signal.
- Il s'agit de l'extension pour les tracés polaires, utilisée pour trouver la stabilité du système de contrôle en boucle fermée.
- C'est un outil extrêmement utile pour déterminer la stabilité du système.
- À l'aide d'un diagramme de Nyquist, nous pouvons surveiller la distance entre les deux points (–1, 0) et le point où la courbe croise l'axe réel négatif.
Comment le diagramme de Nyquist est-il utilisé pour déterminer la stabilité ?
La stabilité peut être déterminée en utilisant Nyquist Plot en regardant simplement le no. d'encerclements du point (−1, 0). La variété des gains sur lesquels le système sera stable peut être déterminée en regardant les croisements d'axes réels. Ce graphique fournit des données concernant la forme de la fonction de transfert.
Que sont les critères de Nyquist pour l'échantillonnage ?
Les critères de Nyquist exigent que la fréquence d'échantillonnage soit au moins deux fois la fréquence maximale contenue dans le signal. Si la fréquence d'échantillonnage est inférieure à deux fois la fréquence de signal analogique la plus élevée, un phénomène appelé crénelage se produira.
Qu'est-ce qui est utilisé pour Nyquist Plot ?
Une fonction de transfert en boucle ouverte est utilisée pour Nyquist Plot.
Qu'est-ce que la règle de Nyquist ?
La règle de Nyquist stipule simplement qu'un signal périodique doit être échantillonné à plus de deux fois la composante de fréquence maximale du signal. En fait, comme le temps disponible est limité, une fréquence d'échantillonnage est quelque peu supérieure à ce qu'elle nécessite.
Qu'est-ce que la formule de débit binaire Nyquist pour Noiseless ?
Nyquist déclare simplement que dans un canal 'B' de bande passante, vous pouvez transmettre jusqu'à 2B signaux orthogonaux pour chaque seconde, donc Rp ≤ 2B, où 'Rp' est la fréquence du pouls.
Que représente l'intrigue de Nyquist ?
Le diagramme de Nyquist représente certaines informations concernant la forme de la fonction de transfert. Ainsi, par exemple; ce graphique donne des informations sur la variation entre le no. des pôles et des zéros de la fonction de transfert par l'angle auquel la courbe atteint l'origine.
Ainsi, ceci est un aperçu de la parcelle de Nyquist – avantages, inconvénients & ses applications. Les tracés de Nyquist sont utilisés pour analyser les propriétés du système de contrôle telles que la stabilité, la marge de phase et la marge de gain. Tracé de Nyquist avec Matlab nous aide à créer un graphique de tracé de Nyquist, lié à la réponse en fréquence générée par un modèle adynamique. Voici une question pour vous, qu'est-ce qu'un complot de Bode?